Simpsonova metoda

Daný interval rozdělíme na sudý počet (2n) MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipv0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaaiikaiaaikdacaWGUbGaaiykaaaa@3915@  stejných subintervalů délky h= b−a 2n MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipv0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiAaiabg2da9maalaaabaGaamOyaiabgkHiTiaadggaaeaacaaIYaGaamOBaaaaaaa@3C79@  . Oblouk křivky původní funkce y=f(x) MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipv0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2da9iaadAgacaGGOaGaamiEaiaacMcaaaa@3B52@  na dvou sousedních subintervalech nahradíme parabolou (interpolačním polynomem druhého stupně), viz. Obr. 1.

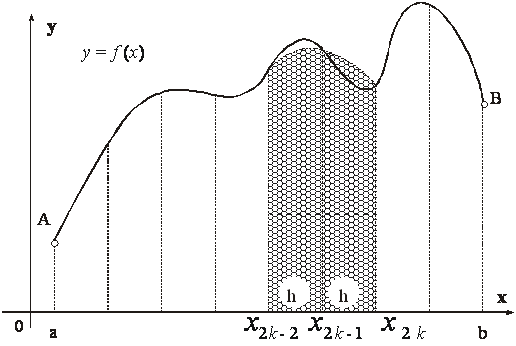
Obr. 1

∫ a b f(x) ⋅dx≈ h 3 (f( x 0 )+f( x 2n )+4(f( x 1 )+f( x 3 )⋯+f( x 2n−1 ))+2(f( x 2 )+f( x 4 )+f( x 2n−2 ))) MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipv0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGceaqabeaadaWdXbqaaiaadAgacaGGOaGaamiEaiaacMcaaSqaaiaadggaaeaacaWGIbaaniabgUIiYdGccqGHflY1caWGKbGaamiEaiabgIKi7cqaamaalaaabaGaamiAaaqaaiaaiodaaaGaaiikaiaadAgacaGGOaGaamiEamaaBaaaleaacaaIWaaabeaakiaacMcacqGHRaWkcaWGMbGaaiikaiaadIhadaWgaaWcbaGaaGOmaiaad6gaaeqaaOGaaiykaiabgUcaRiaaisdacaGGOaGaamOzaiaacIcacaWG4bWaaSbaaSqaaiaaigdaaeqaaOGaaiykaiabgUcaRiaadAgacaGGOaGaamiEamaaBaaaleaacaaIZaaabeaakiaacMcacqWIVlctcqGHRaWkcaWGMbGaaiikaiaadIhadaWgaaWcbaGaaGOmaiaad6gacqGHsislcaaIXaaabeaakiaacMcacaGGPaGaey4kaSIaaGOmaiaacIcacaWGMbGaaiikaiaadIhadaWgaaWcbaGaaGOmaaqabaGccaGGPaGaey4kaSIaamOzaiaacIcacaWG4bWaaSbaaSqaaiaaisdaaeqaaOGaaiykaiabgUcaRiaadAgacaGGOaGaamiEamaaBaaaleaacaaIYaGaamOBaiabgkHiTiaaikdaaeqaaOGaaiykaiaacMcacaGGPaaaaaa@7A93@

Odhad chyby:

Δ S = (b−a) 5 90 n 4 max⁡ <a,b> | f (4) (x) |= n  h 5 90 max⁡ <a,b> | f (4) (x) | MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipv0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeuiLdq0aaSbaaSqaaiaadofaaeqaaOGaeyypa0ZaaSaaaeaacaGGOaGaamOyaiabgkHiTiaadggacaGGPaWaaWbaaSqabeaacaaI1aaaaaGcbaGaaGyoaiaaicdacaWGUbWaaWbaaSqabeaacaaI0aaaaaaakiGac2gacaGGHbGaaiiEamaaBaaaleaacqGH8aapcaWGHbGaaiilaiaadkgacqGH+aGpaeqaaOWaaqWaaeaacaWGMbWaaWbaaSqabeaacaGGOaGaaGinaiaacMcaaaGccaGGOaGaamiEaiaacMcaaiaawEa7caGLiWoacqGH9aqpdaWcaaqaaiaad6gacaaMc8UaamiAamaaCaaaleqabaGaaGynaaaaaOqaaiaaiMdacaaIWaaaaiGac2gacaGGHbGaaiiEamaaBaaaleaacqGH8aapcaWGHbGaaiilaiaadkgacqGH+aGpaeqaaOWaaqWaaeaacaWGMbWaaWbaaSqabeaacaGGOaGaaGinaiaacMcaaaGccaGGOaGaamiEaiaacMcaaiaawEa7caGLiWoaaaa@6981@

V jiném tvaru: Δ S =(b−a)   h 4 90 max⁡ <a,b> | f (4) (x) | MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipv0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeuiLdq0aaSbaaSqaaiaadofaaeqaaOGaeyypa0JaaiikaiaadkgacqGHsislcaWGHbGaaiykamaalaaabaGaaGPaVlaadIgadaahaaWcbeqaaiaaisdaaaaakeaacaaI5aGaaGimaaaaciGGTbGaaiyyaiaacIhadaWgaaWcbaGaeyipaWJaamyyaiaacYcacaWGIbGaeyOpa4dabeaakmaaemaabaGaamOzamaaCaaaleqabaGaaiikaiaaisdacaGGPaaaaOGaaiikaiaadIhacaGGPaaacaGLhWUaayjcSdaaaa@52D8@

Příklad 1.

∫ 0 5 ( e 3x + x 2 3 )dx MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipv0Je9sqWrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaa8qCaeaacaGGOaGaamyzamaaCaaaleqabaGaaG4maiaadIhaaaGccqGHRaWkdaWcaaqaaiaadIhadaahaaWcbeqaaiaaikdaaaaakeaacaaIZaaaaaWcbaGaaGimaaqaaiaaiwdaa0Gaey4kIipakiaacMcacaWGKbGaamiEaaaa@43D2@

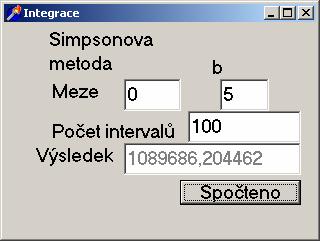
procedure TForm1.Button1Click(Sender: TObject);

var a,b,xi,h,SumaLiche,SumaSude,Meze,Integral:extended;

n, k :integer;

lichy : Boolean ;

begin

  a:=StrToFloat(edit1.text);

  b:=StrToFloat(edit2.text);

  n:=StrToInt(edit3.text);

  Integral:=0;

  h:=(b-a)/(2*n);

  xi:=a;

  SumaLiche :=0;

  SumaSude :=0;

  lichy :=true;

  for k:=1 to 2*n-1 do

  begin

  xi:=xi+h;

  if lichy then

  begin

  lichy:= not lichy;

  SumaLiche := SumaLiche + F(xi);

  end

  else

  begin

  lichy:= not lichy;

  SumaSude := SumaSude + F(xi);

  end;

  Meze :=F(a) +F(b);

  Integral:=h*(Meze+2*SumaSude +4*SumaLiche )/3;

  end;

  edit4.text:=FloatToStr(Integral);

  Button1.Caption:='Spočteno';

end;

Volba kvadraturního vzorce se neřídí nějakými pevnými pravidly. Obvykle ve většině případů vystačíme s užitím lichoběžníkového pravidla. Při větších nárocích na přesnost užijeme zde uváděný Simpsonův vzorec. V některých případech, pokud známe hodnoty druhé, případně třetí derivace funkce v daných bodech, lze spočítat odhad chyby.

Simpsonovo pravidlo konverguje rychleji než lichoběžníkové pravidlo. Protože ve výrazech pro chyby vystupují vyšší derivace, je však lichoběžníkové pravidlo nejlepším vzorcem pro většinu problémů.

Užití vzorců pro určení chyby obdélníkového, lichoběžníkového či Simpsonova pravidla je v mnoha případech nereálné, neboť neznáme maxima absolutní hodnoty příslušných derivací (druhé, třetí či čtvrté) na daném intervalu 〈a,b〉 MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipv0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyykJeUaamyyaiaacYcacaWGIbGaeyOkJepaaa@3C0D@ .