V následující části uvedeme stručně metody určené pro hledání
komplexních a reálných kořenů rovnice, na jejíž levé straně se vyskytuje
polynom stupně
n tehdy, když
a
n
≠0
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipv0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOBaiaabccacaqG0bGaaeyzaiaabIgacaqGKbGaaeyEaiaabYcacaqGGaGaae4AaiaabsgacaqG5bGaaeOFbiaabccacaWGHbWaaSbaaSqaaiaad6gaaeqaaOGaeyiyIKRaaGimaaaa@46A8@
|
a
n
x
n
+
a
n−1
x
n−1
+⋯+
a
1
x
+
a
0
=0
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipv0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyyamaaBaaaleaacaWGUbaabeaakiaadIhadaahaaWcbeqaaiaad6gaaaGccqGHRaWkcaWGHbWaaSbaaSqaaiaad6gacqGHsislcaaIXaaabeaakiaadIhadaahaaWcbeqaaiaad6gacqGHsislcaaIXaaaaOGaey4kaSIaeS47IWKaey4kaSIaamyyamaaBaaaleaacaaIXaaabeaakiaadIhadaahaaWcbeqaaaaakiabgUcaRiaadggadaWgaaWcbaGaaGimaaqabaGccqGH9aqpcaaIWaaaaa@4DE0@
|
(1)
|
Zaměříme se na nejdůležitější
případ, kdy koeficienty
a
n
,
a
n−1
,⋯,
a
1
,
a
0
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipv0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyyamaaBaaaleaacaWGUbaabeaakiaacYcacaWGHbWaaSbaaSqaaiaad6gacqGHsislcaaIXaaabeaakiaacYcacqWIVlctcaGGSaGaamyyamaaBaaaleaacaaIXaaabeaakiaacYcacaWGHbWaaSbaaSqaaiaaicdaaeqaaaaa@4424@
jsou reálná čísla a
x
MathType@MTEF@5@5@+=feaafiart1ev1aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipv0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiEaaaa@370B@
je
komplexní proměnná.
Jak známo, polynomem stupně nula
je každá nenulová konstanta, polynomem jedna pak známá lineární funkce
P(x)=
a
1
x
+
a
0
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipv0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiuaiaacIcacaWG4bGaaiykaiabg2da9iaadggadaWgaaWcbaGaaGymaaqabaGccaWG4bWaaWbaaSqabeaaaaGccqGHRaWkcaWGHbWaaSbaaSqaaiaaicdaaeqaaaaa@3FF7@
a polynomem druhého stupně kvadratická funkce
P(x)=
a
2
x
2
+
a
1
x+
a
0
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipv0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiuaiaacIcacaWG4bGaaiykaiabg2da9iaadggadaWgaaWcbaGaaGOmaaqabaGccaWG4bWaaWbaaSqabeaacaaIYaaaaOGaey4kaSIaamyyamaaBaaaleaacaaIXaaabeaakiaadIhacqGHRaWkcaWGHbWaaSbaaSqaaiaaicdaaeqaaaaa@446A@
Základní věta algebry uvádí, že rovnice
(1)
má n kořenů
α
1
,
α
2
, ...,
α
n
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipv0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeqySde2aaSbaaSqaaiaaigdaaeqaaOGaaiilaiaaykW7cqaHXoqydaWgaaWcbaGaaGOmaaqabaGccaGGSaGaaGPaVlaac6cacaGGUaGaaiOlaiaacYcacqaHXoqydaWgaaWcbaGaamOBaaqabaaaaa@4528@
.
(každý kořen přitom počítáme tolikrát, kolik činí jeho násobnost). Polynom lze
pak přepsat do tvaru
|
P(x)=
a
n
(x−
α
n
)(x−
α
n−1
)⋯(x−
α
1
)
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipv0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiuaiaacIcacaWG4bGaaiykaiabg2da9iaadggadaWgaaWcbaGaamOBaaqabaGccaGGOaGaamiEaiabgkHiTiabeg7aHnaaBaaaleaacaWGUbaabeaakiaacMcacaGGOaGaamiEaiabgkHiTiabeg7aHnaaBaaaleaacaWGUbGaeyOeI0IaaGymaaqabaGccaGGPaGaeS47IWKaaiikaiaadIhacqGHsislcqaHXoqydaWgaaWcbaGaaGymaaqabaGccaGGPaaaaa@51CC@
|
(2)
|
Kořeny rovnice (1)
jsou kořeny polynomu (2).
Někdy se používá též název nulové body
polynomu. Jsou to tedy čísla
α
n
,
α
n−1
,…,
α
1
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipv0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeqySde2aaSbaaSqaaiaad6gaaeqaaOGaaiilaiabeg7aHnaaBaaaleaacaWGUbGaeyOeI0IaaGymaaqabaGccaGGSaGaeSOjGSKaaiilaiabeg7aHnaaBaaaleaacaaIXaaabeaaaaa@42FD@
.
(x−
α
n
),(x−
α
n−1
),⋯,(x−
α
1
)
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipv0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaaiikaiaadIhacqGHsislcqaHXoqydaWgaaWcbaGaamOBaaqabaGccaGGPaGaaiilaiaacIcacaWG4bGaeyOeI0IaeqySde2aaSbaaSqaaiaad6gacqGHsislcaaIXaaabeaakiaacMcacaGGSaGaeS47IWKaaiilaiaacIcacaWG4bGaeyOeI0IaeqySde2aaSbaaSqaaiaaigdaaeqaaOGaaiykaaaa@4D9C@
jsou tzv. kořenoví činitelé
Připomeňme, že kořen
α
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeqySdegaaa@378C@
nazýváme r-násobný
tehdy a jen tehdy, když
f
(r)
(α)≠0∧
f
(j)
(α)=0
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOzamaaCaaaleqabaGaaiikaiaadkhacaGGPaaaaOGaaiikaiabeg7aHjaacMcacqGHGjsUcaaIWaGaey4jIKTaamOzamaaCaaaleqabaGaaiikaiaadQgacaGGPaaaaOGaaiikaiabeg7aHjaacMcacqGH9aqpcaaIWaaaaa@48A8@
pro
j=r−1,…,2,1
MathType@MTEF@5@5@+=feaafiart1ev1aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOAaiabg2da9iaadkhacqGHsislcaaIXaGaaiilaiablAciljaacYcacaaIYaGaaiilaiaaigdaaaa@3F2B@
,
přičemž
f
(j)
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOzamaaCaaaleqabaGaaiikaiaadQgacaGGPaaaaaaa@394D@
značí j–tou
derivaci funkce
f
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOzaaaa@36D8@
Rovnice
x
3
+ x
2
- 5x + 3 = 0
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaaeiEamaaCaaaleqabaGaae4maaaakiaabccacaqGRaGaaeiiaiaabIhadaahaaWcbeqaaiaabkdaaaGccaqGGaGaaeylaiaabccacaqG1aGaaeiEaiaabccacaqGRaGaaeiiaiaabodacaqGGaGaaeypaiaabccacaqGWaaaaa@44BC@
má kořen
α
2
=−3
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeqySde2aaSbaaSqaaiaaikdaaeqaaOGaeyypa0JaeyOeI0IaaG4maaaa@3B2E@
kořen
α
1
=1
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeqySde2aaSbaaSqaaiaaigdaaeqaaOGaeyypa0JaaGymaaaa@3A3E@
dvojnásobný neboť
f
′
(1)=f(1)=0∧
f
″
(1)=8≠0
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGabmOzayaafaGaaiikaiaaigdacaGGPaGaeyypa0JaamOzaiaacIcacaaIXaGaaiykaiabg2da9iaaicdacqGHNis2ceWGMbGbayaacaGGOaGaaGymaiaacMcacqGH9aqpcaaI4aGaeyiyIKRaaGimaaaa@47C0@
Pokud jsou koeficienty
a
n
,
a
n−1
, ⋯,
a
0
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipv0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyyamaaBaaaleaacaWGUbaabeaakiaacYcacaaMc8UaamyyamaaBaaaleaacaWGUbGaeyOeI0IaaGymaaqabaGccaGGSaGaaGPaVlabl+UimjaacYcacaWGHbWaaSbaaSqaaiaaicdaaeqaaaaa@44B3@
reálné, pak se případné komplexní kořeny
vyskytují v komplexně sdružených dvojicích.
Všechny kořeny algebraické
rovnice jsou rozloženy v mezikruží
|
r<| z |<R
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipv0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOCaiabgYda8maaemaabaGaamOEaaGaay5bSlaawIa7aiabgYda8iaadkfaaaa@3E04@
,
|
kde
|
r=
|
a
0
|
a
k
+|
a
0
|
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipv0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOCaiabg2da9maalaaabaWaaqWaaeaacaWGHbWaaSbaaSqaaiaaicdaaeqaaaGccaGLhWUaayjcSdaabaGaamyyamaaBaaaleaacaWGRbaabeaakiabgUcaRmaaemaabaGaamyyamaaBaaaleaacaaIWaaabeaaaOGaay5bSlaawIa7aaaaaaa@44F8@
|
R=1+
a
i
|
a
n
|
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipv0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOuaiabg2da9iaaigdacqGHRaWkdaWcaaqaaiaadggadaWgaaWcbaGaamyAaaqabaaakeaadaabdaqaaiaadggadaWgaaWcbaGaamOBaaqabaaakiaawEa7caGLiWoaaaaaaa@40D2@
|
(3)
|
a
k
je maximální z čísel |
a
n
| , |
a
n−1
| ,⋯ ,|
a
1
| }
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipv0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyyamaaBaaaleaacaWGRbaabeaakiaabccacaqGQbGaaeyzaiaabccacaqGTbGaaeyyaiaabIhacaqGPbGaaeyBaiaabgoacaqGSbGaaeOBaiaab2oacaqGGaGaaeOEaiaabccacaqGneGaaey7aiaabohacaqGLbGaaeiBaiaabccadaabdaqaaiaadggadaWgaaWcbaGaamOBaaqabaaakiaawEa7caGLiWoacaaMc8UaaiilaiaaykW7daabdaqaaiaadggadaWgaaWcbaGaamOBaiabgkHiTiaaigdaaeqaaaGccaGLhWUaayjcSdGaaGPaVlaacYcacqWIVlctcaaMc8UaaiilamaaemaabaGaamyyamaaBaaaleaacaaIXaaabeaaaOGaay5bSlaawIa7aiaaykW7caGG9baaaa@6A00@
,
a
i
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipv0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyyamaaBaaaleaacaWGPbaabeaaaaa@380D@
je maximální z čísel
|
a
n−1
| ,⋯ ,|
a
0
|
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipv0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaaGPaVpaaemaabaGaamyyamaaBaaaleaacaWGUbGaeyOeI0IaaGymaaqabaaakiaawEa7caGLiWoacaaMc8Uaaiilaiabl+UimjaaykW7caGGSaWaaqWaaeaacaWGHbWaaSbaaSqaaiaaicdaaeqaaaGccaGLhWUaayjcSdGaaGPaVdaa@4B58@
Polynom s reálnými koeficienty nemusí mít žádný reálný
nulový bod.
Pro řešení výše uvedené rovnice je vhodné mít představu o počtu
a poloze kořenů algebraické rovnice, které leží v daném intervalu.
Následující text je věnován poloze reálných kořenů.
Pozn.: K řešení uvedené úlohy lze použít již dříve uváděné
metody řešení nelineárních rovnic.
Předpokládáme, že algebraická rovnice
|
a
n
x
n
+
a
n−1
x
n−1
+...+
a
1
x
+
a
0
=0
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipv0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyyamaaBaaaleaacaWGUbaabeaakiaadIhadaahaaWcbeqaaiaad6gaaaGccqGHRaWkcaWGHbWaaSbaaSqaaiaad6gacqGHsislcaaIXaaabeaakiaadIhadaahaaWcbeqaaiaad6gacqGHsislcaaIXaaaaOGaey4kaSIaaiOlaiaac6cacaGGUaGaey4kaSIaamyyamaaBaaaleaacaaIXaaabeaakiaadIhadaahaaWcbeqaaaaakiabgUcaRiaadggadaWgaaWcbaGaaGimaaqabaGccqGH9aqpcaaIWaaaaa@4E08@
;
a
n
>0
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipv0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyyamaaBaaaleaacaWGUbaabeaakiabg6da+iaaicdaaaa@39DE@
|
(4)
|
má pouze jednoduché kořeny.
Při separaci reálných kořenů uvedené rovnice lze užít tzv.
Sturmovu posloupnost:
P(x),
P
1
(x),
P
2
(x),⋯,
P
m
(x)
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipv0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiuaiaacIcacaWG4bGaaiykaiaacYcacaWGqbWaaSbaaSqaaiaaigdaaeqaaOGaaiikaiaadIhacaGGPaGaaiilaiaadcfadaWgaaWcbaGaaGOmaaqabaGccaGGOaGaamiEaiaacMcacaGGSaGaeS47IWKaaiilaiaadcfadaWgaaWcbaGaamyBaaqabaGccaGGOaGaamiEaiaacMcaaaa@4A72@
Získáme ji tak, že položíme
P
1
(x)=
P
′
(x)
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipv0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiuamaaBaaaleaacaaIXaaabeaakiaacIcacaWG4bGaaiykaiabg2da9iqadcfagaqbamaaBaaaleaaaeqaaOGaaiikaiaadIhacaGGPaaaaa@3E9C@
,
dále označíme
P
2
(x)
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipv0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiuamaaBaaaleaacaaIYaaabeaakiaacIcacaWG4bGaaiykaaaa@3A2A@
jako zbytek při dělení
P
(x)
P
1
(x)
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipv0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaacaWGqbWaaSbaaSqaaaqabaGccaGGOaGaamiEaiaacMcaaeaacaWGqbWaaSbaaSqaaiaaigdaaeqaaOGaaiikaiaadIhacaGGPaaaaaaa@3D9A@
násobený číslem
−1
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipv0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyOeI0IaaGymaaaa@37B5@
;
P
3
(x)
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipv0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiuamaaBaaaleaacaaIZaaabeaakiaacIcacaWG4bGaaiykaaaa@3A2B@
je pak zbytek při dělení
P
1
(x)
P
2
(x)
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipv0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaacaWGqbWaaSbaaSqaaiaaigdaaeqaaOGaaiikaiaadIhacaGGPaaabaGaamiuamaaBaaaleaacaaIYaaabeaakiaacIcacaWG4bGaaiykaaaaaaa@3E56@
násobený číslem
−1
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipv0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyOeI0IaaGymaaaa@37B5@
,
atd. Proces tvorby dalších členů ukončujeme v případě, že získáme
konstantu.
Počet reálných kořenů rovnice
a
n
x
n
+
a
n−1
x
n−1
+...+
a
1
x
+
a
0
=0
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipv0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyyamaaBaaaleaacaWGUbaabeaakiaadIhadaahaaWcbeqaaiaad6gaaaGccqGHRaWkcaWGHbWaaSbaaSqaaiaad6gacqGHsislcaaIXaaabeaakiaadIhadaahaaWcbeqaaiaad6gacqGHsislcaaIXaaaaOGaey4kaSIaaiOlaiaac6cacaGGUaGaey4kaSIaamyyamaaBaaaleaacaaIXaaabeaakiaadIhadaahaaWcbeqaaaaakiabgUcaRiaadggadaWgaaWcbaGaaGimaaqabaGccqGH9aqpcaaIWaaaaa@4E08@
na intervalu
<a,b>
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipv0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyipaWJaamyyaiaacYcacaWGIbGaeyOpa4daaa@3A96@
je roven rozdílu mezi počtem znaménkových změn
ve Sturmově posloupnosti pro
x=a
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipv0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiEaiabg2da9iaadggaaaa@38F6@
a
x=b
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipv0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiEaiabg2da9iaadkgaaaa@38F7@
; (
P
(a)⋅
P
(b)≠0
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipv0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiuamaaBaaaleaaaeqaaOGaaiikaiaadggacaGGPaGaeyyXICTaamiuamaaBaaaleaaaeqaaOGaaiikaiaadkgacaGGPaGaeyiyIK7enfgDOvwBHrxAJfwmaeHbnfgDOvwBHrxAJfwmaGqbaiab=bdaWaaa@4AED@
,
tedy
a
MathType@MTEF@5@5@+=feaafiart1ev1aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyyaaaa@36D4@
resp.
b
MathType@MTEF@5@5@+=feaafiart1ev1aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOyaaaa@36D5@
nejsou kořeny mnohočlenu P).
Nechť v rovnici
a
n
x
n
+
a
n−1
x
n−1
+...+
a
1
x
+
a
0
=0
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipv0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyyamaaBaaaleaacaWGUbaabeaakiaadIhadaahaaWcbeqaaiaad6gaaaGccqGHRaWkcaWGHbWaaSbaaSqaaiaad6gacqGHsislcaaIXaaabeaakiaadIhadaahaaWcbeqaaiaad6gacqGHsislcaaIXaaaaOGaey4kaSIaaiOlaiaac6cacaGGUaGaey4kaSIaamyyamaaBaaaleaacaaIXaaabeaakiaadIhadaahaaWcbeqaaaaakiabgUcaRiaadggadaWgaaWcbaGaaGimaaqabaGccqGH9aqpcaaIWaaaaa@4E08@
je
a
n
>0
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipv0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyyamaaBaaaleaacaWGUbaabeaat0uy0HwzTfgDPnwyXaqeg0uy0HwzTfgDPnwyXaacfaGccqWF+aGpcaaIWaaaaa@432C@
Pozn.: Pokud tomu tak není, lze toho jak známo, jednoduše
dosáhnout násobením obou stran rovnice číslem -1
Pro každý reálný kořen
α
MathType@MTEF@5@5@+=feaafiart1ev1aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeqySdegaaa@378D@
rovnice (4)
platí (srovnejte se vztahem (3)):
a)
α<1+
|
ai
|
an
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeqySdeMaeyipaWJaaGymaiabgUcaRmaalaaabaWaaqWaaeaacaWGHbWccaWGPbaakiaawEa7caGLiWoaaeaacaWGHbWccaWGUbaaaaaa@412C@
(Maclaurinův
odhad), kde
|
ai
|
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaqWaaeaacaWGHbWccaWGPbaakiaawEa7caGLiWoaaaa@3AF8@
je nejmenší
záporný (tj. v absolutní hodnotě největší) koeficient v (1); pokud žádný
záporný koeficient neexistuje, je
α≤0
MathType@MTEF@5@5@+=feaafiart1ev1aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeqySdeMaeyizImQaaGimaaaa@39FC@
b)
α<1+
|
ai
|
an
r
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeqySdeMaeyipaWJaaGymaiabgUcaRmaakeaabaWaaSaaaeaadaabdaqaaiaadggaliaadMgaaOGaay5bSlaawIa7aaqaaiaadggaliaad6gaaaaabaGaamOCaaaaaaa@4233@
(Lagrangeův
odhad), kde
|
ai
|
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaqWaaeaacaWGHbWccaWGPbaakiaawEa7caGLiWoaaaa@3AF8@
je opět
nejmenší záporný (tj. v absolutní hodnotě největší) koeficient a
r=n−i
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipv0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOCaiabg2da9iaad6gacqGHsislcaWGPbaaaa@3AD8@
;
i
MathType@MTEF@5@5@+=feaafiart1ev1aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyAaaaa@36DC@
je index
prvního záporného koeficientu v (1)
c)
α<1+
|
ai
|
as
n−(r−s)
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeqySdeMaeyipaWJaaGymaiabgUcaRmaakeaabaWaaSaaaeaadaabdaqaaiaadggaliaadMgaaOGaay5bSlaawIa7aaqaaiaadggaliaadohaaaaabaGaamOBaiabgkHiTiaacIcacaWGYbGaeyOeI0Iaam4CaiaacMcaaaaaaa@4756@
(Tillotův
odhad), kde
a
i
MathType@MTEF@5@5@+=feaafiart1ev1aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyyamaaBaaaleaacaWGPbaabeaaaaa@37EE@
a
r
MathType@MTEF@5@5@+=feaafiart1ev1aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOCaaaa@36E5@
ar
jsou stejné jako v a) a b) a
a
s
MathType@MTEF@5@5@+=feaafiart1ev1aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyyamaaBaaaleaacaWGZbaabeaaaaa@37F8@
je největší
z
n-i
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOBaiaac2cacaWGPbaaaa@387F@
kladných
koeficientů
1. Při řešení algebraické rovnice znalost jednoho kořene
umožňuje snížit stupeň polynomu na levé straně uvažované rovnice.
Algebraická rovnice u níž malé změny koeficientů způsobují
velké změny kořenů, se nazývá špatně podmíněná. Např. pokud v rovnici:
(x-1)(x-2)(x-3)(x-4)(x-5)(x-6)(x-7)(x-8)(x-9)(x-10)
(x-11)(x-12)(x-13)(x-14)(x-15)(x-16)(x-17)(x-18)(x-19)(x-20)=
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGceaqabeaacaGGOaGaamiEaiaac2cacaaIXaGaaiykaiaacIcacaWG4bGaaiylaiaaikdacaGGPaGaaiikaiaadIhacaGGTaGaaG4maiaacMcacaGGOaGaamiEaiaac2cacaaI0aGaaiykaiaacIcacaWG4bGaaiylaiaaiwdacaGGPaGaaiikaiaadIhacaGGTaGaaGOnaiaacMcacaGGOaGaamiEaiaac2cacaaI3aGaaiykaiaacIcacaWG4bGaaiylaiaaiIdacaGGPaGaaiikaiaadIhacaGGTaGaaGyoaiaacMcacaGGOaGaamiEaiaac2cacaaIXaGaaGimaiaacMcaaeaacaGGOaGaamiEaiaac2cacaaIXaGaaGymaiaacMcacaGGOaGaamiEaiaac2cacaaIXaGaaGOmaiaacMcacaGGOaGaamiEaiaac2cacaaIXaGaaG4maiaacMcacaGGOaGaamiEaiaac2cacaaIXaGaaGinaiaacMcacaGGOaGaamiEaiaac2cacaaIXaGaaGynaiaacMcacaGGOaGaamiEaiaac2cacaaIXaGaaGOnaiaacMcacaGGOaGaamiEaiaac2cacaaIXaGaaG4naiaacMcacaGGOaGaamiEaiaac2cacaaIXaGaaGioaiaacMcacaGGOaGaamiEaiaac2cacaaIXaGaaGyoaiaacMcacaGGOaGaamiEaiaac2cacaaIYaGaaGimaiaacMcacqGH9aqpaeaaaaaa@8A73@
2432902008176640000 - 8752948036761600000 x +
13803759753640704000
x
2
- 12870931245150988800
x
3
+
8037811822645051776
x
4
- 3599979517947607200
x
5
+
1206647803780373360
x
6
- 311333643161390640
x
7
+
63030812099294896
x
8
- 10142299865511450
x
9
+
1307535010540395
x
10
- 135585182899530
x
11
+
11310276995381
x
12
- 756111184500
x
13
+ 40171771630
x
14
-
1672280820
x
15
+ 53327946
x
16
- 1256850
x
17
+ 20615
x
18
-
210
x
19
+
x
20
)
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGceaqabeaacaaIYaGaaGinaiaaiodacaaIYaGaaGyoaiaaicdacaaIYaGaaGimaiaaicdacaaI4aGaaGymaiaaiEdacaaI2aGaaGOnaiaaisdacaaIWaGaaGimaiaaicdacaaIWaGaaeiiaiaac2cacaqGGaGaaGioaiaaiEdacaaI1aGaaGOmaiaaiMdacaaI0aGaaGioaiaaicdacaaIZaGaaGOnaiaaiEdacaaI2aGaaGymaiaaiAdacaaIWaGaaGimaiaaicdacaaIWaGaaGimaiaabccacaWG4bGaaeiiaiabgUcaRiaabccaaeaacaaIXaGaaG4maiaaiIdacaaIWaGaaG4maiaaiEdacaaI1aGaaGyoaiaaiEdacaaI1aGaaG4maiaaiAdacaaI0aGaaGimaiaaiEdacaaIWaGaaGinaiaaicdacaaIWaGaaGimaiaabccacaWG4bWaaWbaaSqabeaacaaIYaaaaOGaaeiiaiaac2cacaqGGaGaaGymaiaaikdacaaI4aGaaG4naiaaicdacaaI5aGaaG4maiaaigdacaaIYaGaaGinaiaaiwdacaaIXaGaaGynaiaaicdacaaI5aGaaGioaiaaiIdacaaI4aGaaGimaiaaicdacaqGGaGaamiEamaaCaaaleqabaGaaG4maaaakiaabccacqGHRaWkcaqGGaaabaGaaGioaiaaicdacaaIZaGaaG4naiaaiIdacaaIXaGaaGymaiaaiIdacaaIYaGaaGOmaiaaiAdacaaI0aGaaGynaiaaicdacaaI1aGaaGymaiaaiEdacaaI3aGaaGOnaiaabccacaWG4bWaaWbaaSqabeaacaaI0aaaaOGaaeiiaiaac2cacaqGGaGaaG4maiaaiwdacaaI5aGaaGyoaiaaiMdacaaI3aGaaGyoaiaaiwdacaaIXaGaaG4naiaaiMdacaaI0aGaaG4naiaaiAdacaaIWaGaaG4naiaaikdacaaIWaGaaGimaiaabccacaWG4bWaaWbaaSqabeaacaaI1aaaaOGaaeiiaiabgUcaRiaabccaaeaacaaIXaGaaGOmaiaaicdacaaI2aGaaGOnaiaaisdacaaI3aGaaGioaiaaicdacaaIZaGaaG4naiaaiIdacaaIWaGaaG4maiaaiEdacaaIZaGaaG4maiaaiAdacaaIWaGaaeiiaiaadIhadaahaaWcbeqaaiaaiAdaaaGccaqGGaGaaiylaiaabccacaaIZaGaaGymaiaaigdacaaIZaGaaG4maiaaiodacaaI2aGaaGinaiaaiodacaaIXaGaaGOnaiaaigdacaaIZaGaaGyoaiaaicdacaaI2aGaaGinaiaaicdacaqGGaGaamiEamaaCaaaleqabaGaaG4naaaakiaabccacqGHRaWkcaqGGaaabaGaaGOnaiaaiodacaaIWaGaaG4maiaaicdacaaI4aGaaGymaiaaikdacaaIWaGaaGyoaiaaiMdacaaIYaGaaGyoaiaaisdacaaI4aGaaGyoaiaaiAdacaqGGaGaamiEamaaCaaaleqabaGaaGioaaaakiaabccacaGGTaGaaeiiaiaaigdacaaIWaGaaGymaiaaisdacaaIYaGaaGOmaiaaiMdacaaI5aGaaGioaiaaiAdacaaI1aGaaGynaiaaigdacaaIXaGaaGinaiaaiwdacaaIWaGaaeiiaiaadIhadaahaaWcbeqaaiaaiMdaaaGccaqGGaGaey4kaSIaaeiiaaqaaiaaigdacaaIZaGaaGimaiaaiEdacaaI1aGaaG4maiaaiwdacaaIWaGaaGymaiaaicdacaaI1aGaaGinaiaaicdacaaIZaGaaGyoaiaaiwdacaqGGaGaamiEamaaCaaaleqabaGaaGymaiaaicdaaaGccaqGGaGaaiylaiaabccacaaIXaGaaG4maiaaiwdacaaI1aGaaGioaiaaiwdacaaIXaGaaGioaiaaikdacaaI4aGaaGyoaiaaiMdacaaI1aGaaG4maiaaicdacaqGGaGaamiEamaaCaaaleqabaGaaGymaiaaigdaaaGccaqGGaGaey4kaSIaaeiiaaqaaiaaigdacaaIXaGaaG4maiaaigdacaaIWaGaaGOmaiaaiEdacaaI2aGaaGyoaiaaiMdacaaI1aGaaG4maiaaiIdacaaIXaGaaeiiaiaadIhadaahaaWcbeqaaiaaigdacaaIYaaaaOGaaeiiaiaac2cacaqGGaGaaG4naiaaiwdacaaI2aGaaGymaiaaigdacaaIXaGaaGymaiaaiIdacaaI0aGaaGynaiaaicdacaaIWaGaaeiiaiaadIhadaahaaWcbeqaaiaaigdacaaIZaaaaOGaaeiiaiabgUcaRiaabccacaaI0aGaaGimaiaaigdacaaI3aGaaGymaiaaiEdacaaI3aGaaGymaiaaiAdacaaIZaGaaGimaiaabccacaWG4bWaaWbaaSqabeaacaaIXaGaaGinaaaakiaabccacaGGTaGaaeiiaaqaaiaaigdacaaI2aGaaG4naiaaikdacaaIYaGaaGioaiaaicdacaaI4aGaaGOmaiaaicdacaqGGaGaamiEamaaCaaaleqabaGaaGymaiaaiwdaaaGccaqGGaGaey4kaSIaaeiiaiaaiwdacaaIZaGaaG4maiaaikdacaaI3aGaaGyoaiaaisdacaaI2aGaaeiiaiaadIhadaahaaWcbeqaaiaaigdacaaI2aaaaOGaaeiiaiaac2cacaqGGaGaaGymaiaaikdacaaI1aGaaGOnaiaaiIdacaaI1aGaaGimaiaabccacaWG4bWaaWbaaSqabeaacaaIXaGaaG4naaaakiaabccacqGHRaWkcaqGGaGaaGOmaiaaicdacaaI2aGaaGymaiaaiwdacaqGGaGaamiEamaaCaaaleqabaGaaGymaiaaiIdaaaGccaqGGaGaaiylaiaabccaaeaacaaIYaGaaGymaiaaicdacaqGGaGaamiEamaaCaaaleqabaGaaGymaiaaiMdaaaGccaqGGaGaey4kaSIaaeiiaiaadIhadaahaaWcbeqaaiaaikdacaaIWaaaaOGaaiykaaaaaa@6F93@
změníme-li koeficient
a
19
=−210
MathType@MTEF@5@5@+=feaafiart1ev1aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyyamaaBaaaleaacaaIXaGaaGyoaaqabaGccqGH9aqpcqGHsislcaaIYaGaaGymaiaaicdaaaa@3CAC@
na
a
19
=−(210+
2
−23
)
MathType@MTEF@5@5@+=feaafiart1ev1aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyyamaaBaaaleaacaaIXaGaaGyoaaqabaGccqGH9aqpcqGHsislcaGGOaGaaGOmaiaaigdacaaIWaGaey4kaSIaaGOmamaaCaaaleqabaGaeyOeI0IaaGOmaiaaiodaaaGccaGGPaaaaa@4240@
získáme
|
místo kořenů
|
hodnoty
|
|
14
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaaGymaiaaisdaaaa@3766@
a
15
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaaGymaiaaiwdaaaa@3767@
|
13,9923+2,51881 i
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaaGymaiaaiodacaGGSaGaaGyoaiaaiMdacaaIYaGaaG4maiabgUcaRiaaikdacaGGSaGaaGynaiaaigdacaaI4aGaaGioaiaaigdacaqGGaGaamyAaaaa@42AC@
a
13,9923−2,51881 i
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaaGymaiaaiodacaGGSaGaaGyoaiaaiMdacaaIYaGaaG4maiabgkHiTiaaikdacaGGSaGaaGynaiaaigdacaaI4aGaaGioaiaaigdacaqGGaGaamyAaaaa@42B7@
|
Příklad 1.
Pro reálné kořeny rovnice x3+4x2+x-6=0 získáme odhady:
(n=3;i=0,a0=-6;r=n-0=3,s=2)
a) a<1+
|−6|
1
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipv0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaacaGG8bGaeyOeI0IaaGOnaiaacYhaaeaacaaIXaaaaaaa@3A85@
=7
b) a<1+
|
−6
|
1
3
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipv0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaOqaaeaadaWcaaqaamaaemaabaGaeyOeI0IaaGOnaaGaay5bSlaawIa7aaqaaiaaigdaaaaaleaacaqGZaaaaOGaaeiiaaaa@3D25@
»2,8171
c) a<1+
|
−6
|
4
MathType@MTEF@5@5@+=feaafiart1ev1aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaOaaaeaadaWcaaqaamaaemaabaGaeyOeI0IaaGOnaaGaay5bSlaawIa7aaqaaiaaisdaaaaaleqaaaaa@3BA6@
»2,2247
Descartova věta: Počet kladných kořenů rovnice (4)
je buď roven počtu znaménkových změn v posloupnosti
a
n
,
a
n−1
, ⋯
a
0
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipv0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyyamaaBaaaleaacaWGUbaabeaakiaacYcacaaMc8UaamyyamaaBaaaleaacaWGUbGaeyOeI0IaaGymaaqabaGccaGGSaGaaGPaVlabl+UimjaaykW7caWGHbWaaSbaaSqaaiaaicdaaeqaaaaa@458E@
jeho koeficientů nebo je o sudý počet
menší.
Příklad 2.
K rovnici:
x
4
+3
x
2
-1=0
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipv0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiEamaaCaaaleqabaGaaGinaaaakiabgUcaRiaaiodacaWG4bWaaWbaaSqabeaacaaIYaaaaOGaaeylaiaaigdacqGH9aqpcaaIWaaaaa@3EB9@
sestrojíme příslušnou posloupnost 1,0,3,0,-1,
kde se vyskytuje jedna znaménková změna a rovnice má právě jeden kladný kořen.
Odhady činí:
a) a<2
b) a<2
c) a<1+
|
−1
|
3
MathType@MTEF@5@5@+=feaafiart1ev1aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaOaaaeaadaWcaaqaamaaemaabaGaeyOeI0IaaGymaaGaay5bSlaawIa7aaqaaiaaiodaaaaaleqaaaaa@3BA0@
»1,577
Reálné kořeny jsou: -0,550251 a 0,550251 viz následující
obrázek:
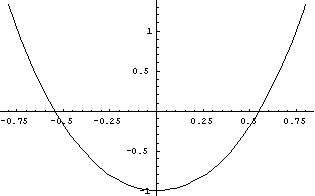
Hodnota kladného kořene, který nás
zajímal, je 0,550251
Newtonova metoda pro
polynomy (Newton-Hornerova metoda,
někdy nazývaná Birge-Veitova metoda)
Velmi často je tato metoda nazývána Newton–Hornerova (na rozdíl
od Newton–Raphsonovy metody pro určení kořenů nelineárních transcendentních
rovnic). Metoda využívá dělení derivací dané funkce (polynomu).
x
j+1
=
x
j
−
P(
x
j
)
P
′
(
x
j
)
MathType@MTEF@5@5@+=feaafiart1ev1aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiEamaaBaaaleaacaWGQbGaey4kaSIaaGymaaqabaGccqGH9aqpcaWG4bWaaSbaaSqaaiaadQgaaeqaaOGaeyOeI0YaaSaaaeaacaWGqbGaaiikaiaadIhadaWgaaWcbaGaamOAaaqabaGccaGGPaaabaGabmiuayaafaGaaiikaiaadIhadaWgaaWcbaGaamOAaaqabaGccaGGPaaaaaaa@467E@
,
kde
P(
x
j
)
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiuaiaacIcacaWG4bWaaSbaaSqaaiaadQgaaeqaaOGaaiykaaaa@3A3D@
je funkční hodnota mnohočlenu a
P
′
(
x
j
)
MathType@MTEF@5@5@+=feaafiart1ev1aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGabmiuayaafaGaaiikaiaadIhadaWgaaWcbaGaamOAaaqabaGccaGGPaaaaa@3A4A@
je hodnota jeho derivace.
Hodnoty polynomu a hodnoty první derivace se efektivně počítají
pomocí známého Hornerova schématu. Základem algoritmu Newtonovy metody pro
polynomy je tedy opakované užití uvedeného Hornerova algoritmu.
Polynom
P
n
(x)=
a
n
x
n
+
a
n−1
x
n−1
+...+
a
1
x
+
a
0
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipv0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiuamaaBaaaleaacaWGUbaabeaakiaacIcacaWG4bGaaiykaiabg2da9iaadggadaWgaaWcbaGaamOBaaqabaGccaWG4bWaaWbaaSqabeaacaWGUbaaaOGaey4kaSIaamyyamaaBaaaleaacaWGUbGaeyOeI0IaaGymaaqabaGccaWG4bWaaWbaaSqabeaacaWGUbGaeyOeI0IaaGymaaaakiabgUcaRiaac6cacaGGUaGaaiOlaiabgUcaRiaadggadaWgaaWcbaGaaGymaaqabaGccaWG4bWaaWbaaSqabeaaaaGccqGHRaWkcaWGHbWaaSbaaSqaaiaaicdaaeqaaaaa@5198@
upravíme do tvaru
P
n
(x)=
((…(
︸
n−1
a
n
x+
a
n−1
)x+
a
n−2
)x+...+
a
2
)x+
a
1
)x+
a
0
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipv0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiuamaaBaaaleaacaWGUbaabeaakiaacIcacaWG4bGaaiykaiabg2da9maayaaabaGaaiikaiaacIcacqWIMaYscaGGOaaaleaacaWGUbGaeyOeI0IaaGymaaGccaGL44pacaWGHbWaaSbaaSqaaiaad6gaaeqaaOGaamiEaiabgUcaRiaadggadaWgaaWcbaGaamOBaiabgkHiTiaaigdaaeqaaOGaaiykaiaadIhacqGHRaWkcaWGHbWaaSbaaSqaaiaad6gacqGHsislcaaIYaaabeaakiaacMcacaWG4bGaey4kaSIaaiOlaiaac6cacaGGUaGaey4kaSIaamyyamaaBaaaleaacaaIYaaabeaakiaacMcacaWG4bGaey4kaSIaamyyamaaBaaaleaacaaIXaaabeaakiaacMcacaWG4bGaey4kaSIaamyyamaaBaaaleaacaaIWaaabeaaaaa@6128@
Někdy je výhodnější přepsat rovnici do tvaru
a
0
x
n
+
a
1
x
n−1
+...+
a
n−1
x+
a
n
=0
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipv0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyyamaaBaaaleaacaaIWaaabeaakiaadIhadaahaaWcbeqaaiaad6gaaaGccqGHRaWkcaWGHbWaaSbaaSqaaiaaigdaaeqaaOGaamiEamaaCaaaleqabaGaamOBaiabgkHiTiaaigdaaaGccqGHRaWkcaGGUaGaaiOlaiaac6cacqGHRaWkcaWGHbWaaSbaaSqaaiaad6gacqGHsislcaaIXaaabeaakiaadIhacqGHRaWkcaWGHbWaaSbaaSqaaiaad6gaaeqaaOGaeyypa0JaaGimaaaa@4DD1@
Polynom upravíme pak takto:
P
n
(x)=
((…(
︸
n−1
a
0
x+
a
1
)x+
a
2
)x+...+
a
n−2
)x+
a
n−1
)x+
a
n
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipv0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiuamaaBaaaleaacaWGUbaabeaakiaacIcacaWG4bGaaiykaiabg2da9maayaaabaGaaiikaiaacIcacqWIMaYscaGGOaaaleaacaWGUbGaeyOeI0IaaGymaaGccaGL44pacaWGHbWaaSbaaSqaaiaaicdaaeqaaOGaamiEaiabgUcaRiaadggadaWgaaWcbaGaaGymaaqabaGccaGGPaGaamiEaiabgUcaRiaadggadaWgaaWcbaGaaGOmaaqabaGccaGGPaGaamiEaiabgUcaRiaac6cacaGGUaGaaiOlaiabgUcaRiaadggadaWgaaWcbaGaamOBaiabgkHiTiaaikdaaeqaaOGaaiykaiaadIhacqGHRaWkcaWGHbWaaSbaaSqaaiaad6gacqGHsislcaaIXaaabeaakiaacMcacaWG4bGaey4kaSIaamyyamaaBaaaleaacaWGUbaabeaaaaa@6128@
Algoritmus výpočtu
P
n
(α)
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipv0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiuamaaBaaaleaacaWGUbaabeaakiaacIcacqaHXoqycaGGPaaaaa@3B03@
,
kde
α
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipv0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeqySdegaaa@37AC@
je dané číslo, je založen na postupném
vypočítávání členů v jednotlivých závorkách. Místo hodnot
α
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipv0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeqySdegaaa@37AC@
dosazujeme jednotlivé hodnoty
x
j
MathType@MTEF@5@5@+=feaafiart1ev1aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiEamaaBaaaleaacaWGQbaabeaaaaa@3806@
.
Rekurentní vzorec je v tomto případě:
b
i
=α
b
i−1
+
a
i
MathType@MTEF@5@5@+=feaafiart1ev1aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOyamaaBaaaleaacaWGPbaabeaakiabg2da9iabeg7aHjaadkgadaWgaaWcbaGaamyAaiabgkHiTiaaigdaaeqaaOGaey4kaSIaamyyamaaBaaaleaacaWGPbaabeaaaaa@4133@
pro
i=1,2,…,n
MathType@MTEF@5@5@+=feaafiart1ev1aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyAaiabg2da9iaaigdacaGGSaGaaGOmaiaacYcacqWIMaYscaGGSaGaamOBaaaa@3D7E@
;
b
0
=
a
0
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOyamaaBaaaleaacaaIWaaabeaakiabg2da9iaadggadaWgaaWcbaGaaGimaaqabaaaaa@3A96@
Výsledek:
P
n
(α)=
b
n
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipv0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiuamaaBaaaleaacaWGUbaabeaakiaacIcacqaHXoqycaGGPaGaeyypa0JaamOyamaaBaaaleaacaWGUbaabeaaaaa@3E0F@
Příklad 3.
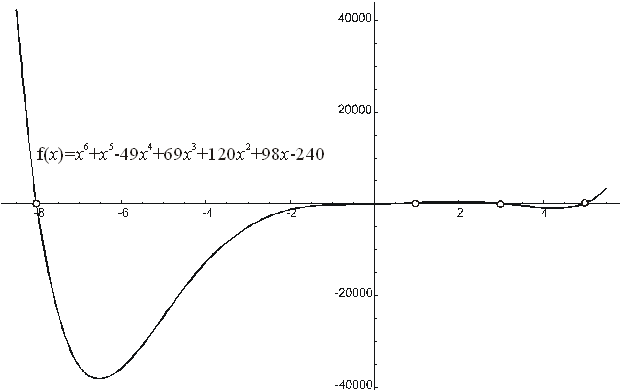
Reálné kořeny jsou:
ξ
1
=−8
MathType@MTEF@5@5@+=feaafiart1ev1aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeqOVdG3aaSbaaSqaaiaaigdaaeqaaOGaeyypa0JaeyOeI0IaaGioaaaa@3B57@
,
ξ
2
=1
MathType@MTEF@5@5@+=feaafiart1ev1aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeqOVdG3aaSbaaSqaaiaaikdaaeqaaOGaeyypa0JaaGymaaaa@3A64@
,
ξ
3
=3
MathType@MTEF@5@5@+=feaafiart1ev1aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeqOVdG3aaSbaaSqaaiaaiodaaeqaaOGaeyypa0JaaG4maaaa@3A67@
,
ξ
4
=5
MathType@MTEF@5@5@+=feaafiart1ev1aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeqOVdG3aaSbaaSqaaiaaisdaaeqaaOGaeyypa0JaaGynaaaa@3A6A@
Program ve Visual Basicu pro Excel:
Sub Newton_Horner()
y_p = 10
y_p_2 = 13
x_p = 0
pocet = Cells(5, 5)
odhad = Cells(1, 1)
x = odhad
For k = 1 To 100
i = 1
bi = Cells(y_p, x_p
+ i)
Cells(y_p + 3, x_p +
i) = bi
For i = 1 To pocet
bi = bi * x +
Cells(y_p, x_p + i + 1)
Cells(y_p + 3, x_p
+ i + 1) = bi
Next i
Cells(6, 5) = bi
i = 1
bi = Cells(y_p_2,
x_p + i)
Cells(y_p + 4, x_p
+ i) = bi
For i = 1 To pocet - 1
bi = bi * x +
Cells(y_p_2, x_p + i + 1)
Cells(y_p + 4, x_p
+ i + 1) = bi
Next i
Cells(6, 7) = bi
odhad = odhad -
(Cells(y_p_2, 7) / Cells(y_p_2 + 1, 6))
Cells(1, 3) = Abs(x -
odhad)
x = odhad
Cells(1, 1) = x
Cells(1, 2) = k
If Cells(1, 3) < 0.0000000001 Then
Exit For
GoTo Konec
End If
Next k
Konec:
End Sub
Obrázek ilustruje stav výpočtu po určení kořene
ξ
4
=5
MathType@MTEF@5@5@+=feaafiart1ev1aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeqOVdG3aaSbaaSqaaiaaisdaaeqaaOGaeyypa0JaaGynaaaa@3A6A@
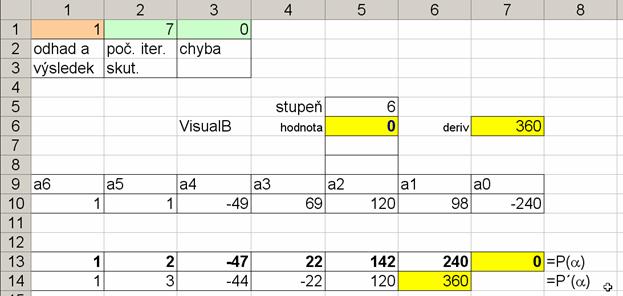
Snížíme-li požadovanou přesnost:
If Cells(1, 3) < 0.000001 Then
Exit For
Je počet iterací o jednu menší

Všimněte si následujícího grafu. Při volbě počátečním odhadu 0
bude určen kořen
ξ
3
=3
MathType@MTEF@5@5@+=feaafiart1ev1aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeqOVdG3aaSbaaSqaaiaaiodaaeqaaOGaeyypa0JaaG4maaaa@3A67@
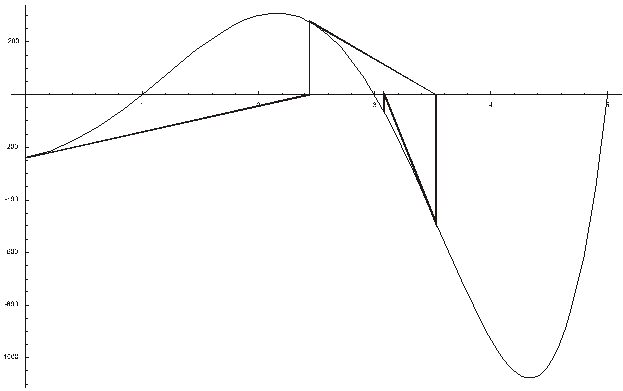
Z obrázku je vidět, že mnohdy velmi záleží na počáteční
aproximaci kořene. Když počáteční aproximace neleží v dostatečné blízkosti
kořene, metoda nemusí konvergovat nebo je určen jiný kořen.
Hledáme-li všechny kořeny rovnice (4),
postupujeme zpravidla tak, že stanovíme její reálný kořen
ξ
1
MathType@MTEF@5@5@+=feaafiart1ev1aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeqOVdG3aaSbaaSqaaiaaigdaaeqaaaaa@3898@
a vydělením levé strany rovnice (4),
tj. mnohočlenu
P
n
(x)
MathType@MTEF@5@5@+=feaafiart1ev1aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiuamaaBaaaleaacaWGUbaabeaakiaacIcacaWG4bGaaiykaaaa@3A42@
lineárním činitelem
x−
ξ
1
MathType@MTEF@5@5@+=feaafiart1ev1aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiEaiabgkHiTiabe67a4naaBaaaleaacaaIXaaabeaaaaa@3A82@
obdržíme rovnici
P
n−1
(x)=0
MathType@MTEF@5@5@+=feaafiart1ev1aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiuamaaBaaaleaacaWGUbGaeyOeI0IaaGymaaqabaGccaGGOaGaamiEaiaacMcacqGH9aqpcaaIWaaaaa@3DAA@
stupně
n−1
MathType@MTEF@5@5@+=feaafiart1ev1aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOBaiabgkHiTiaaigdaaaa@3889@
.
Postup opakujeme s rovnicí
P
n−1
(x)=0
MathType@MTEF@5@5@+=feaafiart1ev1aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiuamaaBaaaleaacaWGUbGaeyOeI0IaaGymaaqabaGccaGGOaGaamiEaiaacMcacqGH9aqpcaaIWaaaaa@3DAA@
.
Získáme kořen
ξ
2
MathType@MTEF@5@5@+=feaafiart1ev1aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeqOVdG3aaSbaaSqaaiaaikdaaeqaaaaa@3899@
.
Pokračujeme do té doby, až dospějeme k rovnici, která nemá reálné kořeny.
Je-li to rovnice druhého stupně, použijeme známý vzorec pro získání komplexních
kořenů.
Existují ještě další specializované metody pro hledání
komplexních a reálných kořenů rovnice, na jejíž levé straně se vyskytuje
polynom stupně
n
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipv0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOBaiaabccaaaa@37A3@
,
jako metoda sečen pro polynomy, Laguerrova metoda, Lehmerova-Schurova metoda či
Grafeova metoda resp. Mullerova metoda. Popis těchto metod přesahuje
rámec tohoto modulu.




