Metoda sečen (sekantová metoda)

Tato metoda je někdy zařazována do skupiny interpolačních metod. Sečna (sekanta) je přímka protínající křivku. Vztah pro metodu sečen lze jednoduše odvodit např. ze vztahu platného pro metodu tečen. Metoda se užívá zejména v případech, kdy derivace f ′ (x) MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipv0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGabmOzayaafaGaaiikaiaadIhacaGGPaaaaa@395A@  je dána příliš složitým vztahem. Nezaměňujte ji však s metodou tětiv! Nekonverguje vždy, je ale stacionární. Oproti metodě regula falsi se (v případě konvergence) jedná o podstatné zlepšení výpočtu. Lze použít následující rekurentní předpis:

x i+1 = y i y i − y i−1 x i−1 + y i−1 y i−1 − y i x i MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipv0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiEamaaBaaaleaacaWGPbGaey4kaSIaaGymaaqabaGccqGH9aqpdaWcaaqaaiaadMhadaWgaaWcbaGaamyAaaqabaaakeaacaWG5bWaaSbaaSqaaiaadMgaaeqaaOGaeyOeI0IaamyEamaaBaaaleaacaWGPbGaeyOeI0IaaGymaaqabaaaaOGaamiEamaaBaaaleaacaWGPbGaeyOeI0IaaGymaaqabaGccqGHRaWkdaWcaaqaaiaadMhadaWgaaWcbaGaamyAaiabgkHiTiaaigdaaeqaaaGcbaGaamyEamaaBaaaleaacaWGPbGaeyOeI0IaaGymaaqabaGccqGHsislcaWG5bWaaSbaaSqaaiaadMgaaeqaaaaakiaadIhadaWgaaWcbaGaamyAaaqabaaaaa@5551@

viz následující obrázek:

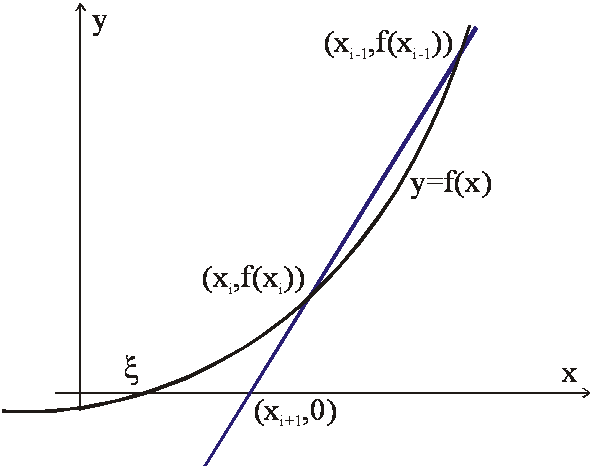
Obr. 1

Ve srovnání s metodou tečen konverguje většinou pomaleji. Metoda je nepoužitelná v případě, že

|f´(x)|≤α MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipv0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaaiiFaiaadAgacaGG0cGaaiikaiaadIhacaGGPaGaaiiFaiabgsMiJkabeg7aHbaa@3FDA@ , kde α MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipv0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeqySdegaaa@37AC@  je číslo blízké nule

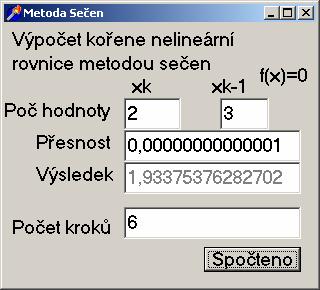
Příklad 1.

( x 2 ) 2 −sin⁡x=0 MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipv0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaeWaaeaadaWcaaqaaiaadIhaaeaacaaIYaaaaaGaayjkaiaawMcaamaaCaaaleqabaGaaGOmaaaakiabgkHiTiGacohacaGGPbGaaiOBaiaadIhacqGH9aqpcaaIWaaaaa@40D4@

Algoritmus:

 

function TForm1.F(X:extended): extended;

begin

F:=(x/2)*(x/2)-Sin(x);

end;

 

procedure TForm1.Button1Click(Sender: TObject);

var Xk,Xk_1,Xk11,fXk,fXk_1,EPS:extended;

k, max_k:integer;

begin

  Xk:=StrToFloat(edit1.text);

  Xk_1:=StrToFloat(edit2.text);

  EPS:=StrToFloat(edit3.text);

 

  max_k := 1000;

  k:=0;

  repeat

   fXk:=F(Xk);

   fXk_1:=F(Xk_1);

   Xk11:=(fXk/(fXk -fXk_1))*Xk_1 +(fXk_1 /(fXk_1 -fXk))*Xk ;

    inc(k);

   Xk_1 := Xk ;

   Xk :=Xk11 ;

  until ((abs (F(Xk11))<EPS) or (k>max_k))  ;

  edit4.text:=FloatToStr(Xk11 );

  Button1.Caption:='Spočteno';

  Edit5.text :=IntToStr(k);

end;